
This paper describes the relations between microstructure, mechanical properties, and electromagneticīehavior of carbon steel wires submitted to different thermomechanical treatments. We show that unlike the considered isotropic mixture rules, which use only the phase volume fraction as the statistical microstructural descriptor, finite element method-based first-order asymptotic homogenization allows prediction of both phase content and directional dependence in the magnetic permeability by permitting an accurate consideration of the underlying phase geometry. The voxel-based discretization of the representative volume element is conducted with digital image processing on the existing micrographs of DP600-grade steel. For the latter, we employ asymptotic homogenization together with the finite element method (FEM) and periodic boundary conditions (PBC). We utilize various mixture rules reported in the literature for the former, some of which correspond to rigorous bounds, e.g., Voigt (arithmetic) and Reuss (harmonic) averages. We investigate the predictive performance of specific analytical and numerical methods to determine the effective magnetic properties of two-phase steels at the macroscale. Based on the trend between incremental permeability and applied magnetic field and the commercial EM sensor (EMspec) operating parameters, the effect of lift-off and hence magnetic field strength on the sensitivity to DP steel properties can be assessed. An analysis of the correlation between coercivity and initial permeability with tensile strength shows that the initial permeability provides a slightly better prediction of strength for the steels examined, which is believed to be due to the fact that a combination of reversible and irreversible domain components affect the coercivity value, while the initial permeability is predominantly affected by reversible domain movements. The effects of ferrite grain size and phase fraction on the incremental permeability are considered, and it has been shown that the influence of ferrite grain boundaries on magnetic permeability is more dominant than the effect of ferrite fraction in commercial DP steel samples. It has been revealed that the incremental permeability increases with the applied magnetic field amplitude to reach a peak and then drops at a higher magnetic field, with the values being different for the three DP grades at a lower field and converging to a similar permeability value at the high field. The ferrite grain sizes and ferrite fractions have been compared with the magnetic parameters obtained from minor and major magnetisation loops within each DP grade. The magnetic properties of commercial dual-phase (DP) steels (DP600, DP800 and DP1000 grades) were evaluated using initial permeability, incremental permeability and coercivity and correlated with the key microstructural differences between the grades. Such differences are beyond the reach of the isotropic effective medium theories, which use only the phase volume fraction and shape as mere statistical microstructural descriptors. In contrast, the disk arrangements in regular square lattices result in the lowest magnetic permeability and inadequate inclusion interaction. Predictions for material systems with monodisperse overlapping disks for a given inclusion volume fraction provide the highest magnetic permeability with the most increased inclusion interaction. Our results with periodic boundary conditions show an excellent agreement with analytical solutions for regular composites, whereas, for random heterogeneous materials, their convergence with volume element size is fast. We show that, for the vanishing corrector function, the derived effective magnetic permeability tensor gives the (lower) Reuss and (upper) Voigt bounds with the vector and scalar potential formulations, respectively. As application problems, 2D regular and random microstructures with overlapping and nonoverlapping monodisperse disks, all of which are periodic, are considered. We propose the use of the meridional eccentricity of the permeability tensor ellipsoid as an anisotropy index quantifying the degree of directionality in the linear magnetic response. Our homogenization algorithm for solving the cell problem is based on the displacement method presented in Lukkassen et al.
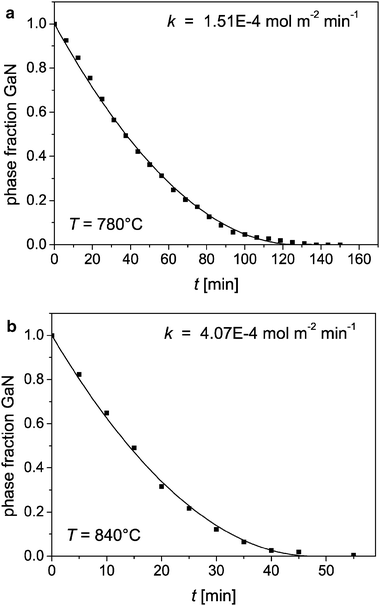
To this end, considering linear magnetostatics, both vector and scalar potential formulations are used. We present a computational framework for two-scale asymptotic homogenization to determine the intrinsic magnetic permeability of composites.


 0 kommentar(er)
0 kommentar(er)
